就像实数模拟直线上的点一样,复数模拟平面上的点。
就几何而言,复数的美妙之处在于它们同时具有两个自然坐标系:笛卡尔坐标系和极坐标系。
在一个重要的背景下,复数是绝对必要的,并且具有物理意义。即量子力学。
如果问题是“复数有什么实际用途?”,那么我们可以指出量子力学的所有无数应用,因为我们知道它们也一定是复数的应用。
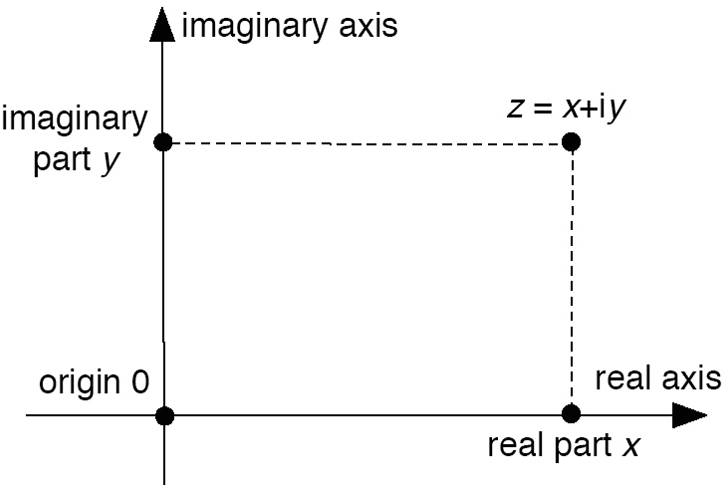


就像实数模拟直线上的点一样,复数模拟平面上的点。
就几何而言,复数的美妙之处在于它们同时具有两个自然坐标系:笛卡尔坐标系和极坐标系。
在一个重要的背景下,复数是绝对必要的,并且具有物理意义。即量子力学。
如果问题是“复数有什么实际用途?”,那么我们可以指出量子力学的所有无数应用,因为我们知道它们也一定是复数的应用。
